Понятие матричного дифференцирования в экономическом анализе

При проведении экономического анализа важно не просто владеть всеми математическими операциями, соответствующим складом ума, ориентироваться в имеющейся информации, но и грамотно пользоваться всеми данными для получения обоснованного и аргументированного вывода. Если Вы полагаете, что достаточно сложить 2 и 2, Вы глубоко ошибаетесь.

Студенты экономического факультета в силу выбранной специальности на протяжении 4-6 лет изучают различные методики проведения экономического анализа. Нет идеального алгоритма, который позволит полностью оценить все стороны предприятия, показать его достоинства и недостатки, выявить проблему. В некоторых случаях приходится комбинировать несколько методик в одну, чтобы получить качественный результат. Знания и навыки нуждаются в постоянных тренировках, поэтому отработку всех способов студенты производят при выполнении контрольных и курсовых работ, во время написания отчета по практике и ВКР.

Одним из самых эффективных и популярных вариантов представления и анализа информации в экономической науке является матричное дифференцирование, о котором мы поговорим в настоящей статье.

Что это такое?

Использование матричного метода предполагает создание специальной матрицы. Сам термин «матрица» пришел в экономическую науку из математики. Внешне матрица выглядит как небольшая прямоугольная таблица. На пересечении строк и столбцов будут находиться конкретные данные, называемые элементами матрицы.

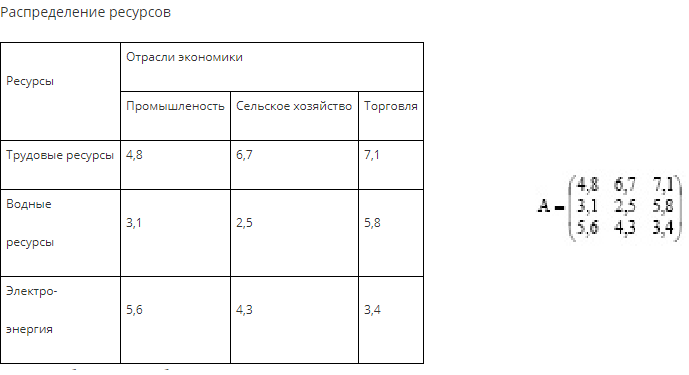
В математической науке матрицы наглядно отражают взаимосвязь разных элементов, их зависимости. Например, имея систему уравнений, можно решить ее с помощью матрицы. В этом случае количество строк будет равно количеству уравнений, а количество столбцов – количеству неизвестных (искомых) параметров.

Матричное дифференцирование предполагает специальное действие над матрицей, которое фактически изменяет ее первоначальный вид, позволяет оценить ее «отклонение». Для реализации дифференцирования разработаны специальные таблицы, упрощающие этот процесс и позволяющие быстро произвести расчеты в большом массиве.

Какие операции можно производить над матрицами?

Математические операции над матрицами стандартны. Их можно складывать и вычитать друг из друга, умножать и делить. Важно использовать при всех операциях одни и те же элементы разных матриц (например, над элементами а11 или а12 и пр.), только с ними производить соответствующие действия. Для перемножения двух матриц важно, чтобы они были соразмерны (имели одинаковое количество строк и столбцов).

Исследователь имеет право менять местами строки и столбцы матрицы. Здесь действует всем известное правило: от перестановки мест слагаемых сумма не меняется.

Существует такое понятие, как транспонирование матрицы. Оно предполагает смены строк на столбцы.

Также специалисты выделяют (и часто пользуется) обратную матрицу – это такая матрица, которая по отношению к изначально составленной таблице при их умножении в результате даст единичную матрицу. Вычисление ее порой дается нелегко и требует массу операций (сложение, вычитание строк и пр.).

На сегодняшний день благодаря Интернет-технологиям произвести расчеты с матрицами и иными любыми данными можно за несколько «кликов мышкой», то в значительной степени облегчает участь специалистов. Но каждый из них должен владеть и ручным способом расчетов.

Применение матриц в экономике

Матричный способ нашел применение не только в математической науке. Сегодня он активно используется специалистами экономической отрасли.

Он позволяет оценить взаимосвязь, зависимость разных величин, исследовать получаемый от использования различных категорий результат, его эффективность. Самым большим преимуществом матричного дифференцирования в экономике является то, что он позволяет представить все сведения в простой форме, быстро произвести нужные операции и получить обоснованный и аргументированный итог. Важно лишь изначально грамотно скомпоновать сведения, обозначить, представить в табличной форме, при необходимости установить систему ограничений и пр.

Возникли сложности?

Нужна помощь преподавателя?

Мы всегда рады Вам помочь!

дипломные
магистерские
диссертации

Чаще всего в матричных экономических моделях находят отражение следующих данных:

• Затраты на производство, распределение продукции и получаемая выгода от ее реализации;
• Взаимосвязь себестоимости и конечного результата, возможности оптимизации;
• Объем отгружаемой продукции, стоимость товара и выручка от реализации и пр.

Использование матриц в экономическом анализе позволяет оценить текущую ситуацию и спланировать дальнейшие действия, которые принесут наибольшую выгоду, смоделировать ситуацию и оптимизировать ее. Достоинством данного метода является быстрое получение конечного результата при помощи действий над матрицами.

Чаще всего рассматриваемая методика успешно применяется при оценке деятельности объекта исследования, прогнозировании экономического развития предприятия или целого региона/отрасли.

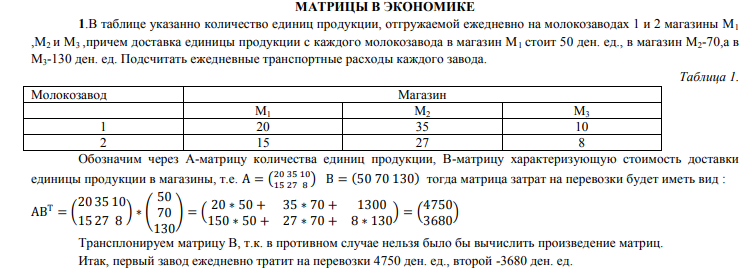
Самый простой способ использования матрицы в экономике – анализ бухбаланса (вычисление отклонений, изменений). Также матричный метод успешно используется при математическом моделировании экономических процессов, например, когда автору курсовой работы предстоит доказать эффективность предлагаемых мероприятий.