
При проведении научного исследования для постановки проблемы важно знать, как она проявляется и что на нее влияет. То есть автору предстоит установить причинно-следственные связи и зависимости определенных переменных, факторов и пр. Не всегда такие моменты можно определить и описать на сугубо словесном, аналитическом уровне. Порой для обоснования результатов и выводов требуется точная информация в виде расчетов, различных показателей и пр. Для этих целей исследователи используют корреляцию: частную и множественную.
СОДЕРЖАНИЕ
Понятие и признаки частной корреляции
Под частной корреляцией понимают особый подход, призванный определить взаимосвязи в определенной области между двумя переменными. При таком способе влияние сторонних факторов, иных переменных не учитывается. То есть здесь исследуется сугубо линейная зависимость.
С помощью этого показателя исследователь определяет, насколько тесной является связь между рассматриваемыми параметрами, если исключить влияние на них извне.
Такой метод не всегда оказывается эффективным и честным, так как он исследует явную зависимость. Не всегда действие одной и той же тактики возможно в разных условиях. Более того, поведение объекта может меняться из-за воздействия на него различных параметров (как внешних, так и внутренних).
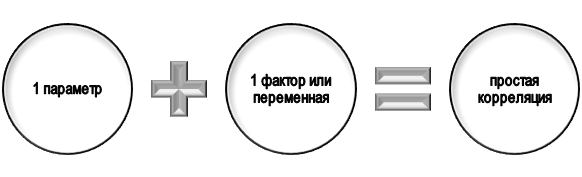
К признакам частной корреляции относят:
- Исследует зависимость строго между двумя параметрами;
- Опирается на расчет парных корреляций;
- Исследует либо влияние одной переменной, либо сразу обеих переменных;
- Значение корреляции находится в ограниченном диапазоне от -1 до +1, действует определенное правило по расшифровке зависимостей: при отрицательном значении прослеживается обратная зависимость переменных, при положительном – прямая. Если показатель корреляции равен 0, то линейной связи между рассматриваемыми параметрами нет.
Притом, чем ближе показатель к 1, тем сильнее и теснее связь между исследуемыми элементами.
Частная корреляция может быть применена при определенных условиях. Во-первых, важно обладать достаточной информацией, чтобы оценить ситуацию. Исследователю желательно ознакомиться с различными материалами и параметрами, чтобы тематически владеть ситуацией и понимать, какие именно тенденции можно исследовать.
Во-вторых, важно оценивать такие переменные, которые находятся в определенной плоскости, диапазоне, шкалах отношений, то есть они должны быть измеримыми. Притом для оценки зависимостей и определения тенденций важно, чтобы измерения были совместимыми или идентичными.
В-третьих, следует учитывать распределение данных. Для подсчета корреляции лучше всего, чтобы оно было нормальным, то есть основная выборка была рядом с усредненным или иным утвержденным для оценки значением (например, дисперсия, медиана, среднее значение показателя и пр.).
В-четвертых, значение корреляции важно перепроверять. Самый простой или классический подход в этом деле – применение р-значения и так называемого доверительного интервала. С их помощью определяется степень случайности связей между исследуемыми параметрами.
Таким образом, частная корреляция – это довольно серьезный инструмент, с помощью которого может определить причины и следствия, сосредоточиться на определенных тенденциях и симптомах, показать связи и особенности их развития в конкретных условиях.
Суть и особенности множественной корреляции
Множественная корреляция представляет собой более сложный процесс, нацеленный на оценку зависимости между переменными, но здесь уже будут учитываться различные факторы. Такой подход позволяет точнее оценить ситуацию и сформировать прогнозы относительно развития ситуации, выработки наиболее эффективного решения для конкретной проблемы.
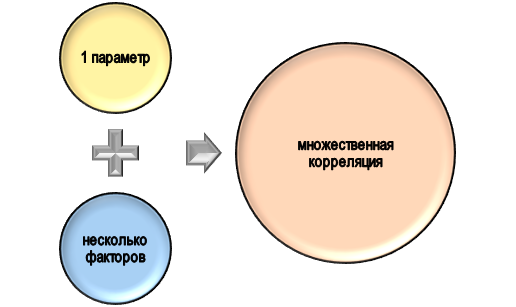
Множественная корреляция позволяет всецело оценить ситуацию и измерить ее:
- Определить основные и потенциальные факторы воздействия. В этом проявляется функция измерения и диагностики,
- Пояснить наличие связей между различными категориями и моментами – описательная функция,
- Определить силу влияния каждого отдельного фактора и их совокупного воздействия на объект. Благодаря такому подходу легко отобрать наиболее сильно воздействующие параметры или подобрать «ключ» к решению проблем на основе факторов-провокаторов. В этом проявляется отборочная миссия,
- Проработать основу для исследования и собрать доказательную базу для обоснования проблемы или решения. В этом состоит функция аргументации и прогноза.
Множественная регрессия бывает различных видов, каждый из которых применим в определенной ситуации и требует соблюдения определенных условий, правил.
Чаще всего студентам доводится работать со следующими типами.
|
Вид |
Общая характеристика |
Условия применения |
| По методике расчета | Оценка зависимостей с учетом особенностей исходной информации, типа связей между категориями | Коэффициент Пирсона – для исследования количественных данных и оценки линейной связи между параметрами Ранговые показатели – для упорядочивания по степени важности, влияния, зависимости порядковых и нелинейных данных |
| По форме зависимости | Позволяет оценить наличие и силу зависимости между несколькими параметрами с учетом факторов воздействия | Линейная корреляция
Нелинейная модель |
| В зависимости от факторного влияния | Модель формируется с учетом определенных факторов, которые берутся исследователем во внимание | Полная – когда учтены все факторы
Последовательная – факторы добавляются по мере необходимости или появления в рамках исследования |
При проведении научного исследования важно тщательно разобраться в исходной информации и подобрать подходящий вид корреляции для оценки зависимостей, связей и пр.
Среди специфических черт множественной корреляции можно отметить следующие характеристики:
- Многофакторность. Исследователь будет всецело изучать материал и ситуацию, выделять все возможные и действующие факторы, воздействующие на объект. Притом студент в ходе НИР может изучать как воздействие отдельных факторов, так и всех выявленных. Такой подход позволяет получить наиболее точные и достоверные результаты, а также сформировать более качественное решение.
- Линейность. С помощью корреляции чаще всего изучают линейные зависимости. В остальных случаях рекомендуется прибегнуть к альтернативным приемам.
- Расшифровка коэффициента корреляции регламентирована. Существует определенный порядок и диапазон для оценки такого показателя. Коэффициент, равный 1 (и все иные значения близкие к 1) свидетельствуют о полной линейной зависимости. Все показатели близкие и равные 0 говорят об отсутствии линейной зависимости между рассматриваемыми параметрами.
- В идеале наблюдается нормальное распределение данных.
- Проверяемость. Чаще всего удостовериться в качестве и точности результаты корреляционного анализа можно с помощью F-теста или методики р-значений с доверительными интервалами.
Множественная корреляция – уникальный показатель многомерного анализа. С его помощью исследователи всецело оценивают ситуацию, определяют основные или все существующие факторы воздействия и учитывают их при построении решения. Благодаря такому анализу легче показать и обосновать наличие противоречия, подобрать рациональный способ его урегулирования.
Как пояснить связь между переменными с помощью корреляции?
Итак, как же правильно расшифровать значение показателя корреляции? С этой задачей справляется не каждый студент. Нередко в ходе исследования допускают ошибки, которые искажают выводы и точность, достоверность результатов.
Напомним, что корреляция подчеркивает наличие связи между рассматриваемыми категориями, но не устанавливает точно причинно-следственные связи. На основе такого показателя можно судить лишь о предсказуемости тенденций, влиянии тех или иных факторов на ситуацию и выдвигать потенциальные решения.
|
Основание для сравнения |
Частная корреляция |
Множественная корреляция |
| Сколько параметров исследуют? | 2 | 3 и более |
| Цель применения | Оценка влияния конкретного параметра на ситуацию, определение вклада переменной в текущую связь | Факторный анализ и выделение наиболее сильно влияющих параметров, оценка влияния каждого отдельного фактора и совокупности факторов, база для прогнозирования |
| Учитывают ли факторы воздействия? | Нет или по минимуму | Учитывают: частично или все полностью |
| Определение причин и следствий | Нет | Нет |
| Определение связи между параметрами | Да | Да |
Чтобы правильно и грамотно описать результаты корреляционного анализа, можно придерживаться следующего плана действий.
Во-первых, нужно тщательно перераспределить имеющийся материал и выделить следующие моменты: переменные, факторы и пр. То есть для начала нужно переработать информационную базу и разобраться в описанной ситуации, наметить основные известные границы, сгруппировать материал и пр. По результатам первого шага студент должен выделить конкретные переменные и факторы, которые он намерен изучать.
Во-вторых, в зависимости от располагаемой исходной информации (ее объема, содержания и т.д.) Нужно постараться понять, какой из показателей корреляции наиболее уместен и эффективен для оценки. Важно изучить правила и условия использования каждого варианта, соотнести с исходной информацией и выбрать определенный вариант. Чаще всего студенты мечутся между коэффициентом корреляции Пирсона, Спирмена, Кендалла, Крамера. Обратите внимание, что у каждого из коэффициентов будет свое обозначение.
В-третьих, расчет показателя и его оценка по шкале корреляции. В ходе исследования универсант на основе располагаемых материалов (посредством их преобразования группировки, переработки и пр.) Должен подсчитать избранный коэффициент корреляции и вывести его итоговое значение. Затем нужно соотнести полученный результат с действующими нормативами.
Если значение коэффициента располагается в диапазоне от -1 до 0, то это говорит о наличии обратной связи между рассматриваемыми переменной и факторами.
Если корреляция лежит в промежутке о 0 до 1, то это говорит о линейной или прямой зависимости данных.
Если же результаты расчетов равны 0, то значит между рассматриваемыми категориями нет никакой связи.
В-четвертых, важно обратить внимание на «знак» корреляции. Если показатель отрицательный, то это значит, что между исследуемыми параметрами прослеживается обратная связь. Она означает, что при увеличении одной из категорий, другая будет уменьшаться.
Если коэффициент корреляции положительный, то наблюдается прямая связь. Она означает, что при увеличении одного из параметров, другие тоже будут расти.
В-пятых, учитывайте не просто диапазон, к которому относится значение корреляции. В зависимости от того, к какому «полю» больше прилегает показатель можно сделать вывод о степени или интенсивности прослеживаемой связи: слабая, средняя (умеренная) или сильная. Чаще всего слабая зависимость видна при корреляции равно от 0,1 до 0,3. Если же показатель находится в промежутке 0,3-0,7, то можно говорить о средней зависимости параметров. При результатах свыше 0,7 – сильная связь между исследуемыми категориями.
В-шестых, обязательно проводите проверку корреляции, чтобы исключить случайности и случайные связи, неточности. Опытные исследователи рекомендуют полагаться на р-значением. Если оно менее 0,05, то такие результаты значимы и не случайны.
В-седьмых, постройте график или диаграмму рассеяния. Визуально наличие связи будет также заметно. Выстраивание точек в восходящем порядке свидетельствует о прямой корреляции и линейной зависимости данных.
Нисходящее расположение точек говорит об обратной зависимости.
Если же точки размещены хаотично и не прослеживается никакой тенденции, то это говорит об отсутствии связи (в этом случае корреляция равно 0).
Важно отметить, что выводы о зависимости делаются только в отношении тех параметров, которые были учтены в уравнении корреляции.
Корреляционный анализ требует не только грамотных расчетов, но и умения их правильно и понятно описать. Поэтому очень важно формулировать все мысли и выводы просто.
Для начала следует отметить, какой именно показатель Вы намерены анализировать или описывать. Для этого можно сделать небольшое вступление или просто отметить, что «На основе расчета показателя корреляции Пирсона…». То есть так мы конкретизируем, какой именно коэффициент был рассчитан и учтен, по необходимости – можно изучить тонкости его подсчета и анализа отдельно.
Затем следует указать полученное вами значение и охарактеризовать его: о чем оно свидетельствует. Для этого достаточно описать вид наблюдаемой связи (исходя из значения показателя и действующих нормативов, правил) и силу зависимости (если она имеется). Также важно указать, между каким параметрами наблюдается обнаруженная связь.
Допустимо в конце анализа отражение уточнений. Например, исследователь может отметить, что указанное им значение корреляции не является абсолютным и не может свидетельствовать и о причинах и следствиях, влиянии иных факторов на ситуацию.
Пример прямой корреляции и ее описания.
В ходе исследования была обнаружена прямая корреляция, равная 0,5 при р менее 0,02. Данный показатель свидетельствует об умеренной зависимости между продолжительность учебы и результатами (успеваемостью) на экзамене. То есть студенты, которые дольше учились и занимались изучением предмета, получали в среднем более высокие отметки в рамках аттестации. Но данный показатель не позволяет сделать выводы о причинно-следственной связи. Не исключается воздействие и иных факторов (например, мотивация, эрудиция, взаимоотношения с педагогом и пр.).
Пример обратной корреляции и ее описания
В рамках корреляционного анализа был рассчитан коэффициент корреляции, равный -0,7 при р менее 0,001. Такой показатель подчеркивает наличие обратной зависимости между рассматриваемыми параметрами: стоимостью товаров и выручкой. При повышении цены объем проданного товара сокращается, что объяснимо с точки зрения экономической теории. Однако, на ситуацию могут влиять и иные факторы. Поэтому для установления причинно-следственных связей необходимо провести дополнительное или более глубокое исследование.
Возникли сложности?
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!

Рекомендации по работе с корреляцией и интерпретацией результатов корреляционного анализа
Корреляционный анализ и расчет соответствующих показателей требует от студентов и исследователей тщательности, осторожности и внимательности.
Изначально разберитесь в понятии, условиях применения, правилах расчета корреляционных коэффициентов. Корреляция – это не 1 показатель, а целая группа различных коэффициентов. Важно различать техники их подсчета, особенности расшифровки и пр.
Не спешите описывать показатель корреляции равный 0, как отсутствие связи. Вполне возможно, что зависимость есть, но она не является линейной. Поэтому следует проводить дополнительные исследования, чтобы убедиться в корректности результатов и выводов.
После подсчета показателя обязательно проведите проверку. Она может сводиться к пересчету или применению альтернативных подходов. Это поможет исключить риск ошибок, случайностей и т.д.
Не стоит однозначно писать, что изменение одного параметра (например, А) вызвано изменением другого аргумента (например, Б). Корреляция – показатель слишком ограниченный. Исследователь не в силах учесть абсолютно все факторы влияния. Старайтесь писать обобщённые выводы, подчеркивающие выявленные тенденции. Судить о причинно-следственных связях на основе корреляции невозможно.
При оценке характера корреляции (слабая, умеренная или сильная) обращайте внимание на предметную область проводимого исследования. То, что в одной науке считается слабым, в другой может относиться к умеренной или сильной.
Старайтесь подчеркивать результаты корреляционного анализа с научной и практической стороны. Научная – поможет описать характер тенденций, а практическая – влияние факторов или общее состояние дел.
Корреляционный анализ предполагает сочетание графиков, таблиц и текста. Важно визуально показать связь, зависимость или ее отсутствие, а затем описать это словесно. Поэтому важно уметь работать с графиками: строить и читать их.
Используйте привычную терминологию. Старайтесь описывать закономерности или результаты НИР в научном стиле, доступно, понятно.
Чаще всего универсанты включают расчет корреляции в аналитический раздел курсовой или дипломной работы. В данном случае оформление материалов будет проводиться согласно общим правилам ГОСТ, регламентирующим ход написания проекта.
Для получения наиболее точной картины опытные исследователи рекомендуют сначала рассчитать частную, а затем множественную корреляцию. В первом случае будут исключены лишние моменты. Автор сможет сосредоточиться на конкретном вопросе, условиях. Расширение параметров поможет учесть влияние извне и составить более качественные рекомендации по решению проблемы с учетом установленных зависимостей. Так студент соберет достаточную доказательную базу для обоснования идеи.
Трудности с учебой?
Требуется поддержка?
Помощь в написании студенческих и
аспирантских работ!







