Учимся быстро считать в уме: основные лайфхаки

Математика – царица наук, которая немыслима без точности и закономерностей, строгих правил и законов, последовательности действий. Далеко не каждому учащемуся изучение математических дисциплин дается легко. Здесь требуется не просто знание чисел и операций над ними, но и умение анализировать полученный результат.

Ключевыми итерациями в математике являются действия над числами: сложение, вычитание, умножение и деление. Если с умножением можно совладать, вызубрив таблицу умножения, то с остальными операциями придется попотеть.

Сегодня мы расскажем о самых действенных методиках, которые облегчат подсчеты в уме.

С чего начать?

Не торопитесь приступать к изучению методик, которые позволят мгновенно складывать многозначные числа. Для начала необходимо «собрать базу». Тренируйте мозг, начиная от простого и следуя к более сложному.

Первым делом необходимо довести до автомата простейшие операции. Начните со сложения однозначных чисел, а затем переходите на двузначные. После того, как сможете довести до «автомата» простые итерации и действия, получать правильный ответ в течение 1-2 секунд, можно переходить на следующий уровень.

Учимся складывать многозначные числа

Самый простой и эффективный способ сложения многозначных чисел – это разбиение их на составные части, простые для сложения или вычитания.

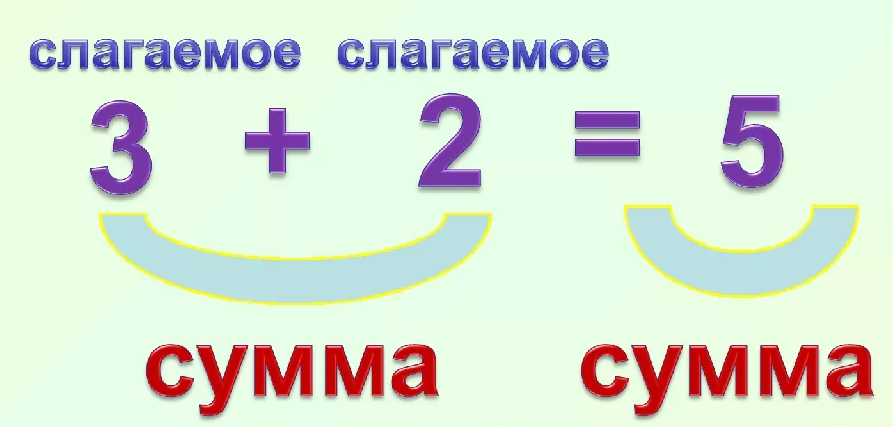
Например, давайте суммируем числа 256 и 685. С виду пример кажется сложным, но на самом деле его можно решить в течение 1-2 минут без калькулятора! Для этого достаточно представить каждое слагаемое в виде простых элементов:

256 = 200+50+6

685 = 600+80+5

Далее останется лишь сложить между собой простые элементы и получить ответ:

256+685 = (200+600)+(50+80)+(6+5)= 800+130+11 = 941

Данный способ посилен даже школьнику. Благодаря ему можно складывать разные числа в уме, быстро и просто, без калькуляторов и прочих дополнительных гаджетов. Правда, для быстрого проведения всех необходимых действий необходимо чаще тренироваться.

Возникли сложности?

Нужна помощь преподавателя?

Мы всегда рады Вам помочь!

дипломные
магистерские
диссертации

Учимся вычитать числа в уме

Здесь алгоритм действий немного иной. Можно прибегнуть к разбиению чисел на составные части, но применять это способ целесообразно не ко всем элементам, а лишь к вычитаемому параметру.

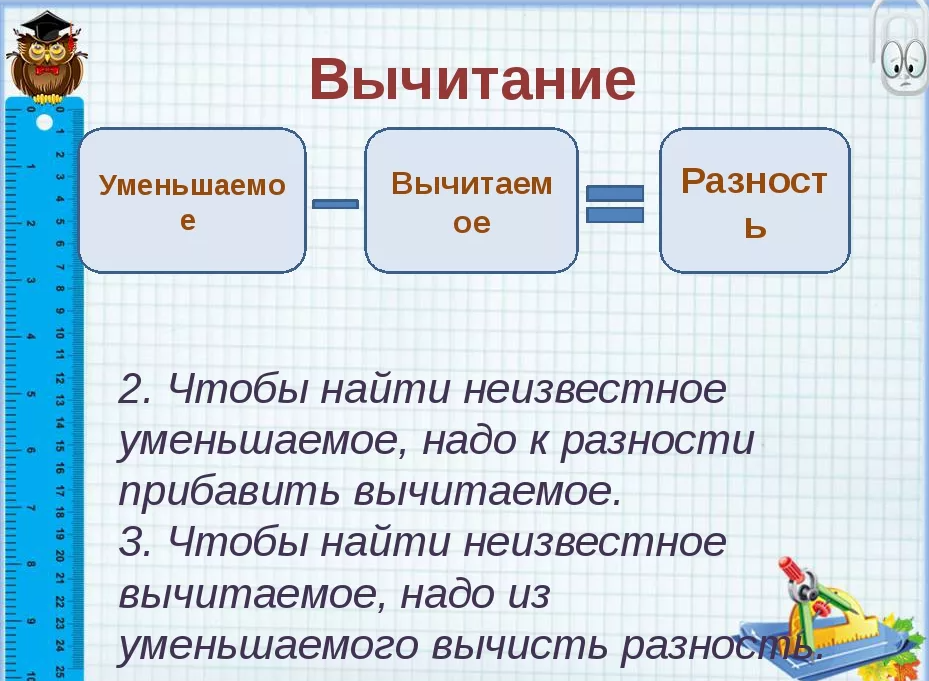
Например, нам нужно решить пример: 761-255.

Чтобы произвести действия в уме достаточно разбить на составные части число 255.

255 = 200+55 = 200+50+5

Теперь останется провести простые операции: 761-200-55 = 561-50-5 = 511-5 = 506

Учимся перемножать числа

Операция умножения базируется на знании таблицы умножения. Поэтому для начала необходимо выучить таблицу умножения, а далее можно приступать к решению примеров, основываясь на принципе «от простого к сложному».

Притом в умножении также можно прибегать к расчленению сложных чисел на более простые элементы.

Рассмотрим действие этого правила на примере: 532*7.

Разобьем число 532 на составные части: 500, 30 и 2.

Останется перемножить каждое число на 7 и сложить полученные результаты: 500*7+30*7+2*7 = 3500+210+14 = 3724

При умножении двузначных чисел можно также разбить один из множителей на составные части.

25*32, представим 32 как 30 и 2.

Далее останется провести следующие операции: 25*30+25*2 = 750+50 = 800

Учимся делить в уме

Деление в уме – самое сложное. Здесь важно владеть всеми предшествующими действиями. Чтобы упростить операции, нужно иметь представление: что на что можно делить, как можно представить сложные числа в более простом для деления виде.

Например, 1024 : 8. Можно делить «столбиком» или представить 1024 на простые составные части, которые в уме можно быстро разделить на 8.

1024 = (800+160+64) : 8 = 800:8 + 160:8 + 64:8 = 100+20+8 = 128

При делении на двузначное число нужно пользоваться интуицией и определять границы допустимых значений. Например, нам нужно решить пример: 1476 : 12. Определяем примерные границы, прикинув какое число нужно умножить на 12, чтобы получить близкое к делимому значение. Получим, что ответ на указанный пример будет в диапазоне от 120 до 130. Далее обращаем внимание на окончание делимого числа 1476 (6 и 76), подбираем потенциальное окончание, исходя из таблицы умножения, и получим 123. Проверяем 123*12 = 1476.

Указанные методики – не единственные в своем роде. Можно подобрать наиболее удобный и понятый для каждого человека способ. Например, в математической науке применяют метод Гаусса, матричные методы, системы уравнений, методы подстановки, замены и пр.

Чтобы быстро решать примеры разного уровня сложности в уме, нужно постоянно тренироваться. Начинайте с простых примеров и постепенно усложняйте задачи. Придумывайте примеры на ходу или пользуйтесь учебниками. Подобные тренировки позволяют развить не только умение считать, но и повышают внимание, концентрацию, развивают и укрепляют память.

Упрощайте любые сложные задания, ведь решить маленькие проблемы гораздо проще и быстрее, чем бороться в мегамасштабной преградой.